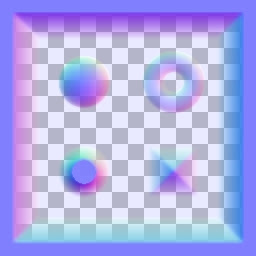
В этой статье своей целью я ставлю попытку, по своему, раскрыть суть данного эффекта, более подробно и доступно чем это делалось ранее, кем бы то ни было и с реализацией на XNA GS. Так, что бы было понятно начинающим. По максимуму охватить опорные моменты и используемые инструменты, а так же из собственного опыта нюансы, которые могут возникнуть.

И так поехали.
Для чистоты эксперимента рассмотрим частный случай.
Описание условий эксперимента:
Объект – (Поверхность текстурирования) плоскость, квадрат.
Расположение объекта – (изначальное) параллельно плоскости экрана, лицом к камере.
Карта нормалей – (текстура) для ее построения используем расчет, приведенный в моей статье
«Calculation deep normal map».
Нам потребуется новый тип описания формата вершин, назовем его VertexPositionTangentSpaceTexture.
(код его реализации)
public struct VertexPositionTangentSpaceTexture
{
public Vector3 Position;
public Vector3 Normal;
public Vector3 Binormal;
public Vector3 Tangent;
public Vector2 TextureCoordinate;
public static readonly VertexElement[] VertexElements;
static VertexPositionTangentSpaceTexture()
{
VertexElements = new VertexElement[5];
short offset = 0;
// Position
VertexElements[0] = new VertexElement(
0, offset,
VertexElementFormat.Vector3,
VertexElementMethod.Default,
VertexElementUsage.Position,
0);
offset += (short)Marshal.SizeOf(new Vector3());
// Normal
VertexElements[1] = new VertexElement(
0, offset,
VertexElementFormat.Vector3,
VertexElementMethod.Default,
VertexElementUsage.Normal,
0);
offset += (short)Marshal.SizeOf(new Vector3());
// Binormal
VertexElements[2] = new VertexElement(
0, offset,
VertexElementFormat.Vector3,
VertexElementMethod.Default,
VertexElementUsage.Binormal,
0);
offset += (short)Marshal.SizeOf(new Vector3());
// Tangent
VertexElements[3] = new VertexElement(
0, offset,
VertexElementFormat.Vector3,
VertexElementMethod.Default,
VertexElementUsage.Tangent,
0);
offset += (short)Marshal.SizeOf(new Vector3());
// TextureCoordinate
VertexElements[4] = new VertexElement(
0, offset,
VertexElementFormat.Vector2,
VertexElementMethod.Default,
VertexElementUsage.TextureCoordinate,
0);
}
public VertexPositionTangentSpaceTexture(
Vector3 position,
Vector3 normal,
Vector3 binormal,
Vector3 tangent,
Vector2 textureCoordinate)
{
this.Position = position;
this.Normal = normal;
this.Binormal = binormal;
this.Tangent = tangent;
this.TextureCoordinate = textureCoordinate;
}
public static int SizeInBytes
{
get
{
return (int)( Marshal.SizeOf(new Vector3()) +
Marshal.SizeOf(new Vector3()) +
Marshal.SizeOf(new Vector3()) +
Marshal.SizeOf(new Vector3()) +
Marshal.SizeOf(new Vector2()));
}
}
}
В его описании поля: Normal, Binormal и Tangent. Послужат нам описанием локальной системы координат для каждой вершины, так называемый tangent space – пространство косательной. В данном примере мы не будем ударятся в оптимизацию и экономию. Потому для наглядности примера используем все три вектора и тем самым заострим внимание на самой сути Bump Map’инга и возможно это помежет кому либо избежать подводных камней при изучении этого примера.
Генерируем поверхность с вершинами типа VertexPositionTangentSpaceTexture.
(пример)
public void Quad()
{
float y0 = 0.5f;
float y1 = -y0;
float x0 = -0.5f;
float x1 = -x0;
float z0 = 0.5f;
float z1 = -z0;
z0 = 0; z1 = 0;
verts = new VertexPositionTangentSpaceTexture[4];
indices = new int[6];
int iv, ii;
iv = 0;
ii = 0;
// front
verts[iv + 0].Position = new Vector3(x0, y0, z0);
verts[iv + 1].Position = new Vector3(x1, y0, z0);
verts[iv + 2].Position = new Vector3(x0, y1, z0);
verts[iv + 3].Position = new Vector3(x1, y1, z0);
verts[iv + 0].Normal = Vector3.Backward;
verts[iv + 1].Normal = Vector3.Backward;
verts[iv + 2].Normal = Vector3.Backward;
verts[iv + 3].Normal = Vector3.Backward;
verts[iv + 0].Binormal = Vector3.Up;
verts[iv + 1].Binormal = Vector3.Up;
verts[iv + 2].Binormal = Vector3.Up;
verts[iv + 3].Binormal = Vector3.Up;
verts[iv + 0].Tangent = Vector3.Right;
verts[iv + 1].Tangent = Vector3.Right;
verts[iv + 2].Tangent = Vector3.Right;
verts[iv + 3].Tangent = Vector3.Right;
verts[iv + 0].TextureCoordinate = Vector2.Zero;
verts[iv + 1].TextureCoordinate = Vector2.UnitX;
verts[iv + 2].TextureCoordinate = Vector2.UnitY;
verts[iv + 3].TextureCoordinate = Vector2.One;
indices[ii + 0] = iv + 0;
indices[ii + 1] = iv + 1;
indices[ii + 2] = iv + 2;
indices[ii + 3] = iv + 2;
indices[ii + 4] = iv + 1;
indices[ii + 5] = iv + 3;
iv += 4;
ii += 6;
// verts
vertexBuffer = new VertexBuffer(
graphics.GraphicsDevice,
VertexPositionTangentSpaceTexture.SizeInBytes * verts.Length,
BufferUsage.None);
vertexBuffer.SetData
(verts);
// index
indexBuffer = new IndexBuffer(
graphics.GraphicsDevice,
sizeof(int) * indices.Length,
BufferUsage.None, IndexElementSize.ThirtyTwoBits);
indexBuffer.SetData(indices);
vertexDeclaration = new VertexDeclaration(graphics.GraphicsDevice, VertexPositionTangentSpaceTexture.VertexElements);
}
}
Обращаю Ваше внимание на инициализацию опять же Normal, Binormal и Tangent. Фишка в том, что по условиям эксперимента я заранее знаю как будет расположен в пространстве текстурируемый объект. Потому так же знаю как будет расположенна нормаль к его лицевой стороне и соответствующие ей Binormal и Tangent.
В случае же со сложной, изогнутой поверхностью с большим количеством треугольников нам прийдется выполнять не простые вычисления для расчета tangent space к каждой вершине. Так же учитывать углы между плоскостями треугольников с общими вершинами и либо усреднять tangent space при малых углах, либо добовлять новые вершины для разделения значений tangent space соответствующие этим же треугольникам при углах близких к 90 градусам. Но это уже развитие идеи и большая тема для отдельной статьи.
Для чего нам это нужен tangent space?
Все просто. Как вы наверно знаете, в вершинном шейдере при обычном текстурировании, для правильного проецирования в плоскость экрана, мы выполняем следующие преобразования:
(пример)
Out.Position = mul( In.Position, matWVP );
Out.Light = normalize( vLight );
Out.Normal = normalize( mul( In.Normal, matWorld ) );
Out.Texcoord = In.Texcoord;
Т.е.
- преобразуем и проецируем координаты вершины в плоскость экрана матрицей matWVP (семантика :WORLDVIEWPROJECTION);
- преобразуем нормали матрицей matWorld (семантика :WORLD) – поворот нормалей для правильного расчета освещения в пиксельном шейдере;
Но в нашем случае нормали к вершинам поворачивать мы не будем. Потому, что это влечет за собой поворот всех нормалей, к каждому пикселю текстуры, принадлежащих выводимым треугольникам, а это лишние действия. Классический прием - поворот вектора освещения обратно повороту объекта, вот так:
(пример)
float3 vLight = mul(vLightPos, matWorldBack) - In.Position;
//float3 tangent = float3(1,0,0); \
//float3 binormal = float3(0,1,0); - в нашем частном случае
//float3 normal = float3(0,0,1); /
float3 normal = normalize(In.Normal);
float3 binormal = normalize(In.Binormal);
float3 tangent = normalize(In.Tangent);
float3x3 matTS = float3x3(tangent, binormal, normal);
Out.vLightTS = normalize(mul(vLight, matTS));
Мы поворачиваем вектор источника света vLightPos в соответствии с преобразованиями накопленными в матрице matWorldBack. Эта матрица является обратной матрицей для мировой матрицы объекта. Прернос и масштабирование в данном случае нас не интересуют, потому как vLightPos вектор, а не координата, и мы нормализуем итоговый результат.
Что значит обратная матрица? Матрица в которой собраны преобразования обратные оригинальной матрице. В данном случае с помощью обратной матрицы мы вращаем вектор освещения в сторону обратную вращению нашего объекта.
Получить обратную матрицу средствами XNA очень просто:
matWorldBack = Matrix.Invert(matWorld);
Далее переводим координаты источника света (в статичную!) локальную систему координат очередной вершины действиями:
float3 normal = normalize(In.Normal);
float3 binormal = normalize(In.Binormal);
float3 tangent = normalize(In.Tangent);
float3x3 matTS = float3x3(tangent, binormal, normal);
Out.vLightTS = normalize(mul(vLight, matTS));
Где, matTS – матрица описывающая tangent space вершины.
После чего мы готовы к текстурированию с учетом освещения и псевдо рельефа.
В пиксельном шейде (пример):
float4 ps(PS_INPUT In) : COLOR0
{
float3 vNormalTS = tex2D( sTexture0, In.Texcoord ) * 2 - 1;
float4 color = float4(0.8f, 0.8f, 0, 1);
float3 vlightTS = In.vLightTS;
float light = clamp(dot(vNormalTS, vlightTS), 0, 1);
return mul(color, light);
}
Стоит обратить внимание на две строчки:
1) float3 vNormalTS = tex2D( sTexture0, In.Texcoord ) * 2 - 1;
где, мы берем нормаль к поверхности в данном пикселе текстуры и распаковываем ее в первоначальный вид, т.к. в normal map у нас хранятся данные о (естественно) нормалях, но упакованными по условной формуле:
color = normal * 0.5f + vector(0.5f, 0.5f, 0.5f);
Подробнее смотреть статью о расчете - «Calculation deep normal map».
2) float light = clamp(dot(vNormalTS, vlightTS, 0, 1);
сам расчет интенсивности освещения для данного пикселя текстуры.
(полный пример шейдера)
float4x4 matWorld : WORLD0;
float4x4 matWorldBack : WORLD1;
float4x4 matWVP : WORLDVIEWPROJECTION0;
float3 vLightPos;
float3 vViewPos;
struct VS_INPUT
{
float3 Position : POSITION0;
float3 Normal : NORMAL0;
float3 Binormal : BINORMAL0;
float3 Tangent : TANGENT0;
float2 Texcoord : TEXCOORD0;
};
struct VS_OUTPUT
{
float4 Position : POSITION0;
float2 Texcoord : TEXCOORD0;
float3 vLightTS : TEXCOORD3;
};
VS_OUTPUT vs( VS_INPUT In )
{
float3 vLight = mul(vLightPos, matWorldBack) - In.Position;
float3 normal = normalize(In.Normal);
float3 binormal = normalize(In.Binormal);
float3 tangent = normalize(In.Tangent);
float3x3 matTS = float3x3( tangent, binormal, normal );
VS_OUTPUT Out = ( VS_OUTPUT ) 0;
Out.Position = mul(float4( In.Position, 1 ), matWVP);
Out.Texcoord = In.Texcoord;
Out.vLightTS = normalize(mul(vLight, matTS));
return Out;
}
texture tex0;
sampler2D sTexture0 = sampler_state
{
Texture = (tex0);
MinFilter = LINEAR;
MagFilter = LINEAR;
MipFilter = LINEAR;
AddressU = CLAMP;
AddressV = CLAMP;
};
struct PS_INPUT
{
float2 Texcoord : TEXCOORD0;
float3 vLightTS : TEXCOORD3;
};
float4 ps(PS_INPUT In) : COLOR0
{
float3 vNormalTS = tex2D( sTexture0, In.Texcoord ) * 2 - 1;
float4 color = float4(0.8f, 0.8f, 0, 1);
float3 vlightTS = In.vLightTS;
float light = clamp(dot(vNormalTS, vlightTS), 0, 1);
return mul(color, light);
}
{
pass Pass_0
{
VertexShader = compile vs_2_0 vs();
PixelShader = compile ps_2_0 ps();
}
}
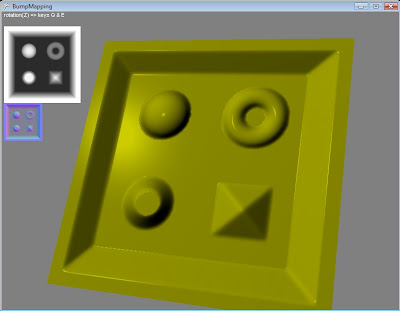
Результат:

Абсолютно прозрачные и простые примеры это хорошо. Но закончить статью хочется ярче. Потому поковыряв в приложении к RenderMonkey пример «Parallax Occlusion Mapping». Я добавил бликовую модель освещения и тут же картинка (ее можно увидеть в начале статьи) стала живее.
(пример шейдера)
float4x4 matWorld : WORLD0;
float4x4 matWorldBack : WORLD1;
float4x4 matWVP : WORLDVIEWPROJECTION0;
float3 vLightPos;
float3 vViewPos;
struct VS_INPUT
{
float3 Position : POSITION0;
float3 Normal : NORMAL0;
float3 Binormal : BINORMAL0;
float3 Tangent : TANGENT0;
float2 Texcoord : TEXCOORD0;
};
struct VS_OUTPUT
{
float4 Position : POSITION0;
float2 Texcoord : TEXCOORD0;
float3 vNormalWS : TEXCOORD1;
float3 vViewWS : TEXCOORD2;
float3 vLightTS : TEXCOORD3;
float3 vViewTS : TEXCOORD4;
};
VS_OUTPUT vs( VS_INPUT In )
{
float3 vLight = mul(vLightPos, matWorldBack) - In.Position;
float3 vViewDir = mul(vViewPos, matWorldBack) - In.Position;
float3 normal = normalize(In.Normal);
float3 binormal = normalize(In.Binormal);
float3 tangent = normalize(In.Tangent);
float3x3 matTS = float3x3( tangent, binormal, normal );
VS_OUTPUT Out = ( VS_OUTPUT ) 0;
Out.Position = mul(float4( In.Position, 1 ), matWVP);
Out.Texcoord = In.Texcoord;
Out.vNormalWS = In.Normal;
Out.vViewWS = vViewDir;
Out.vLightTS = normalize(mul(vLight, matTS));
Out.vViewTS = normalize(mul(vViewDir, matTS));
return Out;
}
texture tex0;
sampler2D sTexture0 = sampler_state
{
Texture = (tex0);
MinFilter = LINEAR;
MagFilter = LINEAR;
MipFilter = LINEAR;
AddressU = CLAMP;
AddressV = CLAMP;
};
struct PS_INPUT
{
float2 Texcoord : TEXCOORD0;
float3 vNormalWS : TEXCOORD1;
float3 vViewWS : TEXCOORD2;
float3 vLightTS : TEXCOORD3;
float3 vViewTS : TEXCOORD4;
};
float4 cSpecularColor = float4(1, 1, 1, 1);
float fSpecularExponent = 300;
float4 ps(PS_INPUT In) : COLOR0
{
float3 vNormalTS = tex2D( sTexture0, In.Texcoord ) * 2 - 1;
float4 color = float4(0.8f, 0.8f, 0, 1);
float3 vlightTS = In.vLightTS;
float3 vReflectionTS = normalize( 2 * dot( In.vViewTS, vNormalTS ) * vNormalTS - In.vViewTS );
float fRdotL = dot( vReflectionTS, In.vLightTS );
float4 cSpecular = saturate( pow( fRdotL, fSpecularExponent )) * cSpecularColor;
float light = clamp(dot(vNormalTS, vlightTS) * (color + cSpecular), 0, 1);
return mul(color, light);
}
technique BumpMapping
{
pass Pass_0
{
VertexShader = compile vs_2_0 vs();
PixelShader = compile ps_2_0 ps();
}
}
Скачать пример можно тут (требуется регистрация xnadev.ru) (чуть позже, в оригинальном блоге, ссылка станет доступна)
Оригинал блога